第4回 回避軌道を“数学的に”求めよう
この円軌道とは、実際にはどういう軌道なのかをこれから求めてみたいと思います。ここからは純粋な数学です。数学の問題らしく表現すると、こんなふうになります。

「傾きはゼロ」とは、クルマは最初まっすぐ前を向いていますよということを、数学的に表現したものです。
普通、数学では右向きを x、上向きを y としますけれども、今日は下向きを y として考えてください。
自分のクルマから見て座標 (xp,yp) が障害物の位置です。この円 Cp の半径が r です。クルマは原点 O にいて、まっすぐ前を向いている。障害物がここにあって、車幅の半分の円を描くとこうなる。求めたいのは、これに外接する円の半径 Rです。
では、この円の中心はどこにあるでしょう。点 O における円の接線がx方向、つまり真横向きなので、円の中心はこの真下のどこかにあるということがわかります。
その中心を C としましょう。「この点 C と点 O の距離を、xp とか yp とか r を使って表しなさい」というのが問題となっています。
実は、これは簡単に求まります。どうするかというと、この青い三角形に注目します。こういう幾何学の問題は、補助線をうまく引くと簡単に求めることができます。

こういうふうに三角形を考えると、三角形の辺の1つはそのまま xp です。もう1つ辺は、O から C までが R ですが、Cp の y 座標が yp ですので、辺の長さはR-yp となります。
最後に、この直角三角形の斜辺は、R+r となっています。
直角三角形といえば、三平方の定理、あるいはピタゴラスの定理、a2+b2=c2 です。この三角形について、三平方の定理を考えればいいわけです。 まず、a2 が xp2 で、b2 が (R-yp)2 、 c2 が(R+r)2 です。よって、

という等式が成り立ちます。これを展開して R について整理すると、半径 R が
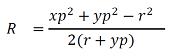
という数学的に美しい式として出てくるわけですね。 まだ問題は終わってはいません。この円弧 OS の中心角 θ も求めなければいけません。この角度は、高校1年生くらいで習う数学のサイン、コサイン、タンジェントのタンジェントを使って、あの直角三角形に着目すると、以下の式で表されます。

高校の数学だと、この θ の値を求めるのは、ものすごく大変なんですけれども、計算機を使えば一瞬で答えは出ます。この式の R は先ほど求めたもので、さらに、xp、yp という障害物の位置も代入して、あとは計算機に入れれば、簡単に計算してくれます。

円弧 SF についても、高校の数学で同じようにして解くことができます。





