第3回 障害物をギリギリで避けるには ~“ギリギリ”の解明

ポイントは「ギリギリで避ける」ということですが、では、“ギリギリ”とは何でしょうか。頭の中では直感的にわかると思いますが、数学的に厳密に考えるとしたら、どういう定義になるのでしょうか。
障害物と道路境界(壁)のどちらにも当たらずに通り抜けることを考えた場合、最初に思いつくのが、こんな感じだと思います。
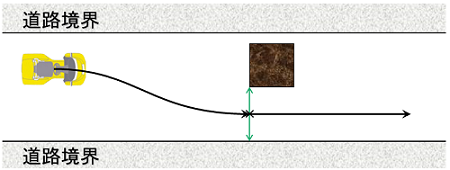
もちろん、これも正解の一つです。こういう避け方もありますが、今日考えたいのは、もっとギリギリです。
レースゲームをやったことのある人はわかると思いますが、素早く通り抜けるには、障害物の端に当たるか当たらないか、壁の方も当たるか当たらないかのギリギリを通るのが良いです。じゅうぶん余裕を持って通るのではなくて、障害物や壁をかするような感じが「ギリギリで避けている」ということになります。

ギリギリが見えた
ギリギリというのを、もうちょっと厳密に考えてみましょう。障害物をギリギリで避けているクルマの軌跡を6つあげます。次の6台のクルマは、どれもギリギリで障害物には当たらずに走っていいます。
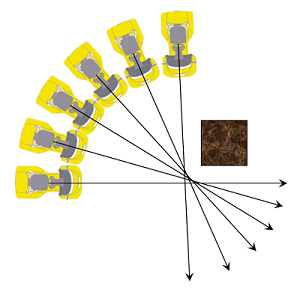
このようなギリギリのクルマの動きを集めると、障害物とクルマの軌跡の間に、なにか円が見えてきませんか。数学的に考えていくと、下図の青い円の中に車両の軌跡、つまりクルマの中心が通った跡が入っていなければ、障害物には当たらないということになります。逆にいうと、青い円の中に線が入ってしまうような動き方をすると、障害物に当たってしまいます。

この青い円とはいったい何でしょうか。実は、この青い円の中心は、この障害物の端っことなっています。青い円の半径は、クルマの幅の半分です。したがって、この青い円は、障害物の端を中心とした、半径が車幅の半分である円、といえます。その円の中に、このクルマの軌跡が入っていなければ、クルマは障害物を避けられます。
今日私たちが求めたいのは、この青い円の中に入らない車両の軌道のうち、ハンドル操作が一番小さいもの、つまり、青い円内に入らず、なおかつ最も旋回半径の大きい軌道ということになります。絵で表すと、こんな感じですね。

青い円の中に線が入っていないもののうち、できるだけ半径が大きいもの。つまり、外側から2番目の曲線のように車両を動かせば、一番小さなハンドル操作で障害物を避けられるということになります。
私たちが今求めるのは、この青い円に接するような円軌道です。もっと厳密に数学っぽくいうと、この青い円に外接する円、ということになります。
油断大敵。壁はどうする?
障害物を避ける問題としてはここまでですが、クルマとして考えた場合、こちら側にも壁があります。このまま走っていくと壁にぶつかってしまうので、どこかで左旋回に切り替えて、壁にぶつからないようにしないといけません。
それがどこかは、答えは一つではありませんが、先ほど紹介した私たちが考えた未来のぶつからないクルマのシステムでは、青い⇒の部分としています。

車両の軌道の円と、この青い円が接する所、これを接点といいますが、この接点を越えたら、クルマはもう障害物には当たりません。あとは壁にぶつからないことだけを考えれば良いので、この接点まで来たらハンドルを左に戻しましょう。
どういうふうにハンドルを戻すかの正解もいろいろありますが、ここまでこういう半径で来たのだから、ここからも、逆向きで同じ半径の円を描いていけば、ハンドル操作の量はこれまでと同じになります。この赤線のように、最初の実線の方の円に沿ってここまで行って、そこから先は点線の方の円に乗り換えて走っていく、というのが私たちの答えです。





