ランダムな数って何？それは、デタラメに選ばれた乱数。人間が作為しない数ってこと。しかし、どんなランダムな乱数を作っても、すごい情報処理能力を持ったコンピュータが、特徴を見つけてしまったら、ランダムじゃなくなるのかな？計算理論の河村先生は、「真にランダムな乱数は作れるのか？」というナゾに迫ります。

ばれなきゃいい？見破られないランダムな数字は作れるのか

ランダムって何？という話をします。例えば0～1までの範囲内でランダムな数を選べという問題を考えてみます。一般にランダムとは無作為のことです。でも人間が無作為に選んだといっても、いかにもそこに作為があるようでわざとらしい。そこでサイコロを無限回振ってみることにします。

するとデタラメっぽい数字ができました。でもよく見ると、ある繰り返し（法則性）が発見できます。一番上の数字は、「389380」という有限な数字列の繰り返しです。

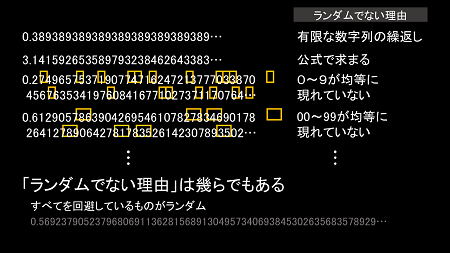
何万桁も数字がバラバラに出てくるπ（円周率）は、どうでしょう。πはランダムでしょうか。円周率は特別な数です。そういうふうに書き方で表せるようなものは、そもそもランダムじゃありません。

その下の「0・27496575371…」は「7」が頻繁に出てきて、0～9が均等に現れていないので、やはりランダムじゃない。「0・6129057863…」は、「78」が頻繁に出て、00～99までが均等に現れておらず、これもランダムじゃありません。このようにいくらランダムに作ったとしても、ランダムじゃないという理由はいくらでも考えられるわけです。

少しまとめてみましょう。ランダムとは、でたらめを作る側でなく、見る側の問題なのではないか、と考えられます。これを計算理論の世界では、ランダムとは「どんな方法で見ても特徴が見つからないような数」と定義します。

そうなると、誰に見つからないかという話になります。それは、見破ろうとする人の情報処理能力に応じてではないでしょうか。それでランダムの概念は決まります。つまり、誰かにバレなきゃランダムだという話です。これが擬似乱数の考え方です。

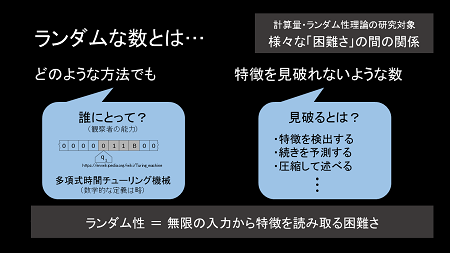
例えば暗号で乱数を使おうと思った時に、必要なのは、その暗号を破ろうとする悪い人にバレなきゃいいということです。その悪い人は、神様でなく人間ですから、無限に先まで見られない。人間の情報処理には限界がある、だからそれをだませればいいということです。

ランダムの面白い点は、数を見る側が、与えられた無限のものから何かを取り出すということに関する難しさにあります。私が取り組んでいるのは、そういう難しさの間の関係を知りたいということです。検出するのと、予測するのとどっちが難しいか、それが少しずつわかってきました。詳しく話したかったのですが、今日はちょっと時間が有限なので、この辺で終わりにしますね。

この分野はどこで学べる？