複数配送手段のより良いルートを最適化理論で高速計算

ドローンと船 どう使うといちばん良いか
遠くの初めての駅に行くとき、路線検索で「どこで乗り換えれば最短で着くかな?」と調べるようなことがあると思います。このような「最短ルートを見つける計算」は、宅配便のルート作りの計算にも利用されています。
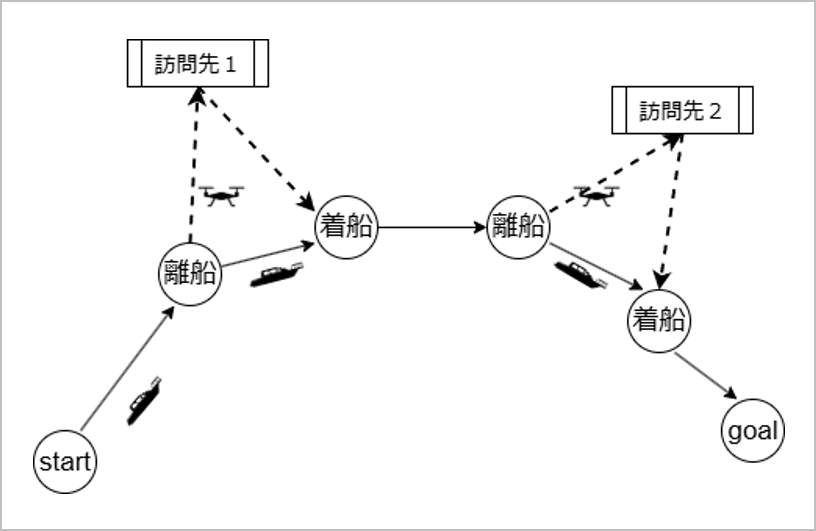
いま研究しているのは、ドローンと船が連携するような協同配送です。ドローンは船より速いけれど飛行距離が短く、船はゆっくりでも遠くまで運べる。複数の離島に配送するときに、どこでドローンを船から飛ばして、どこで戻ってくるようにするのがいちばん良いのか、選択肢は膨大です。ここで数理最適化の出番となります。
数学の面白さとコンピュータの面白さ
数理最適化は複数の選択肢からベストなものを数学の理論に基づいて探す研究分野ですが、ドローンの飛行座標をコンピュータ上で計算するために錐最適化理論と呼ばれる理論を用いてプログラムを作っています。
錐最適化理論は対象となる問題の構造をどれだけ上手く利用できるかで、同じベストな結果を見つけるのでもコンピュータ上で計算にかかる時間が1000秒から1秒まで短くなったりします。どれだけ計算時間を短くできるか、まるでパズルをやっているような面白さがあります。
数理最適化は、数学の理論で考えてコンピュータで試す、つまり数学の面白さとコンピュータの面白さ、一粒で二度おいしい。通学の乗り換えや文化祭での役割分担など、“全体が良くなる一手”を考えることが数理最適化へとつながっています。
もともと錐最適化理論を研究していましたが、ドローンと船が連携するような協同配送に興味を持ったのは、海外の研究者から「錐最適化理論がこんなふうに使われているよ」と教えてもらったことがきっかけです。
数理最適化はいろんな分野とつながっているので、いろんな研究者と共同研究できるところが面白い。以前は錐最適化理論を使って遺伝子関係の最適化計算の研究も行っていましたが、これも海外の研究者に教えてもらった内容がベースになっています。
「錐最適化理論に基づく協同配送ルート最適化問題に対する数値解法の開発」
◆ 山下研究室HP

◆主な業種
(1) ソフトウエア、情報システム開発
(2) 金融・保険・証券・ファイナンシャル
(3) コンサルタント・学術系研究所
◆主な職種
(1) システムエンジニア
(2) 基礎・応用研究、先行開発
(3) 設計・開発
簡単なニューラルネットワーク(2入力、2出力で中間層が1層程度)で学習する場合に、最急降下法で計算した場合とNesterovの加速法で計算した場合にどれくらい計算時間が変わるかを比較してみましょう。
| Q1.日本以外の国で暮らすとしたらどこ? 夏は韓国で冬は台湾で暮らしたい。共同研究でお世話になったし、両方ともご飯がおいしい。 |
|
| Q2.学生時代に/最近、熱中したゲームは? サガ・フロンティア2:サガフロ2は人生だから。いろんなことの節目で「あのときのセリフはこういう意味だったのか」とわかるようになったりすることがある。 |
|
| Q3.好きな言葉は? Live as if you were to die tomorrow. Learn as if you were to live forever. |






